まずはこれを見てください
わずか8×8=64個のドット。この小さな世界で、単純なルールに従って「セル(マス目)」が生き、死に、増殖します。
これは 「セル・オートマトン(Cellular Automaton)」 と呼ばれる、数学的な生命シミュレーションです。
今回は、以前紹介した 74HC595とドットマトリクスLEDの制御技術 をさらに進化させ、2次元セル・オートマトン に挑戦しました。また、前回の 1次元セル・オートマトン で扱った「Rule 30」などとは異なり、今回は 周囲8マスを見て次の状態を決定する より複雑なルールを実装しています。
システム構成
使用パーツ
今回使用しているのは、前回の記事で紹介した 自作のドットマトリクスLEDシールド基板 です。
- Arduino Nano / UNO
- ドットマトリクスLEDシールド基板(74HC595×2、ドライバIC、8×8LED搭載)
この基板には以下が実装されています:
- 74HC595 シフトレジスタ × 2個(SPI通信でデータ受信)
- TBD62783 / TBD62083(ドライバIC:大電流駆動用)
- 8×8ドットマトリクスLED(OSL641501-ARA)

システム全体の構成
自作基板の入手方法
オープンソースで公開中(無料): 回路図、基板データ、プログラムはすべてGitHubで公開しています。JLCPCBでそのまま実装依頼可能なBOM/CPLファイルも含まれています。
完成品を購入: 基板発注の手間を省きたい方は、完成キット(IC・抵抗実装済み)をBoothで販売しています。
詳しい基板の設計や製作過程については、74HC595とドットマトリクスLED制御の記事をご覧ください。
描画の仕組み:SPI + ダイナミック点灯
8×8=64個のLEDを制御するには、本来64本のピンが必要です。しかし、前回の記事で解説した通り、74HC595シフトレジスタ と ダイナミック点灯 を組み合わせることで、わずか 3本のピン(SPI通信) だけで制御できます。
74HC595とは?
74HC595 は、シリアルデータをパラレル出力に変換するシフトレジスタICです。Arduino側からSPI通信で8ビットのデータを送ると、IC側で8本の出力ピンに変換してくれます。
今回は2個のIC を数珠つなぎ(カスケード接続)して、合計16ビット(2バイト)のデータを送信し、以下のように使い分けています:
- 1個目のIC: 8行のうち、どの行を点灯させるか選択(行選択用)
- 2個目のIC: 選択された行の中で、どの列を点灯させるかのパターン(列パターン用)
ダイナミック点灯
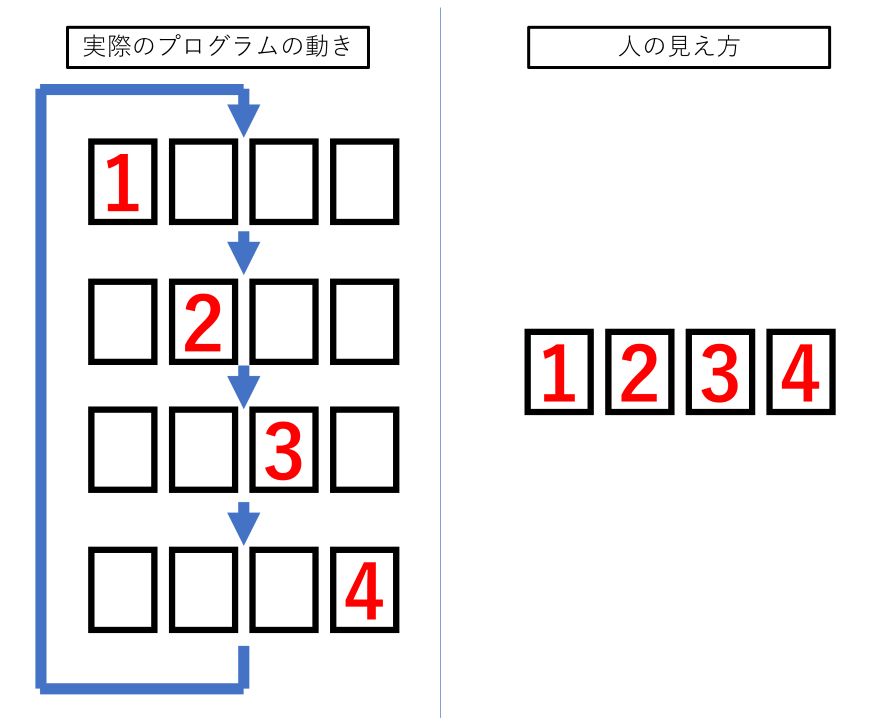
ダイナミック点灯の仕組み
全てのLEDを同時に点灯させるのではなく、1行ずつ順番に高速点灯 させます。
時刻0ms: 1行目だけON → [パターンA]
時刻2ms: 2行目だけON → [パターンB]
時刻4ms: 3行目だけON → [パターンC]
...
このサイクルを 1秒間に数百回 繰り返すと、人間の目には全体が同時に光っているように見えます。これが 残像効果 を利用した「ダイナミック点灯」です。
詳しい仕組みは、74HC595とドットマトリクスLEDの記事をご覧ください。
工夫した点:8x8でも「動き続ける世界」を作る
2次元セル・オートマトンの中で最も有名なのは 「ライフゲーム(Conway’s Game of Life)」 です。しかし、ライフゲームを含む多くのルールには共通の問題があります。
問題: 数世代経つと、画面が「静止した形(ブロック、点滅パターンなど)」に落ち着いてしまい、動きが止まる。
特に 8×8という極小画面 では、この問題が顕著です。広大な画面なら複雑なパターンが長時間続きますが、狭い画面では数秒で安定してしまいます。
解決策:グローバル・ドリフト(Global Drift)
そこで今回、「画面全体を定期的に横にシフトさせる」 という機能を実装しました。
// 5世代ごとに画面全体を1ピクセル横にシフト
if (generationCount % 5 == 0) {
shiftWorld();
}
void shiftWorld() {
for (int i = 0; i < 8; i++) {
byte lastBit = (world[i] >> 7) & 1; // 右端のビットを取得
world[i] = (world[i] << 1) | lastBit; // 左シフトして右端に戻す
}
}
これにより、端の判定が常に変わり、永遠に連鎖反応が続く「死なない世界」 を実現しました。
また、一定確率で ランダムなドットを反転 させる「ノイズ注入」も実装しています。これは宇宙の塵のように、突発的な進化のきっかけを与えます。
4つの生命ルール
動画で映える、性格の違う4つのアルゴリズムを実装しました。各ルールは 約10秒ごとに自動切り替わり し、切り替え時には数字が表示されます。
| 番号 | ルール名 | 特徴 | 視覚的イメージ |
|---|---|---|---|
| 1 | Maze(迷路) | 触手が伸びるように線が広がり、複雑な幾何学模様を作る | 🌿 迷路、血管、樹木の枝 |
| 2 | Coral(サンゴ) | 塊がじわじわと成長し、有機的な島のような形を作る | 🪸 サンゴ礁、結晶成長 |
| 3 | Seeds(火花) | 爆発的な増殖と消滅を繰り返す、最もダイナミックなモード | 💥 火花、爆発、連鎖反応 |
| 4 | Classic(ライフゲーム) | おなじみのルール。安定と変化のバランスが美しい | 🧬 生命の誕生と死 |
ルール1: Maze(迷路)
case MAZE:
nextAlive = alive ? (neighbors >= 1 && neighbors <= 4) : (neighbors == 3);
break;
- 生きているセル: 周囲に1〜4個の生きたセルがあれば生存
- 死んでいるセル: 周囲にちょうど3個あれば誕生
このルールは 細い線が伸びていく 特性があり、迷路のような複雑なパターンを作り出します。

Mazeルールのパターン:触手のように伸びる線
ルール2: Coral(サンゴ)
case CORAL:
nextAlive = alive ? (neighbors >= 4 && neighbors <= 8) : (neighbors == 3);
break;
- 生きているセル: 周囲に4〜8個あれば生存(過密でも死なない)
- 死んでいるセル: 周囲にちょうど3個あれば誕生
Mazeよりも 塊が残りやすく、サンゴ礁や結晶のような有機的な成長を見せます。
Coralルールのパターン:サンゴ礁のような有機的な塊
ルール3: Seeds(火花)
case SEEDS:
nextAlive = (neighbors == 2);
break;
- すべてのセル: 周囲にちょうど2個あれば誕生、それ以外は死ぬ
このルールは 爆発的な増殖 を引き起こします。生きたセルは次の世代で必ず死にますが、周囲に2個あると新たなセルが生まれるため、火花が飛び散るような連鎖反応 が続きます。

Seedsルールのパターン:爆発的な増殖と消滅
ルール4: Classic(ライフゲーム)
case CLASSIC:
nextAlive = alive ? (neighbors == 2 || neighbors == 3) : (neighbors == 3);
break;
- 生きているセル: 周囲に2〜3個あれば生存
- 死んでいるセル: 周囲にちょうど3個あれば誕生
これは1970年に数学者ジョン・コンウェイが考案した 「ライフゲーム」 の標準ルールです。
前回の1次元セル・オートマトンの記事では、ルール30やルール110などの「1次元」を扱いましたが、ライフゲームは 「2次元」 であり、より複雑な生命らしい振る舞いを見せます。

ライフゲームのパターン:安定と変化のバランス
実装のハイライト
① ルール切り替え時の「数字表示」
今どのルールが動いているか一目でわかるよう、切り替え時に ミラー補正済みのフォント で「1, 2, 3, 4」をカウント表示しています。
const byte numFonts[4][8] = {
{0x08, 0x0C, 0x08, 0x08, 0x08, 0x08, 0x1C, 0x00}, // 1
{0x1C, 0x22, 0x20, 0x10, 0x08, 0x04, 0x3E, 0x00}, // 2
{0x1C, 0x22, 0x20, 0x18, 0x20, 0x22, 0x1C, 0x00}, // 3
{0x10, 0x18, 0x14, 0x12, 0x3F, 0x10, 0x10, 0x00} // 4
};
8×8ドットマトリクスLEDには 「ミラー(鏡像)問題」 があります。これは、LED側から見た配線と、ユーザー側から見た向きが左右反転しているため、そのまま表示すると数字が反転してしまう問題です。
ドットマトリクスLEDの記事でも解説しましたが、フォントデータを事前に左右反転させておくことで、正しい向きで表示されるようにしています。
② 「動かない世界」を壊す:グローバル・ドリフト
前述の通り、5世代ごとに画面全体を1ピクセル横に強制シフトさせることで、静止した形を崩し、永遠に動き続ける世界 を実現しました。
③ ノイズ(宇宙の塵)の注入
// 強めのノイズ注入(時々新しい生命の種をまく)
if (random(100) < 10) {
world[random(8)] ^= (1 << random(8));
}
10%の確率でランダムなドットを反転させることで、突発的な進化を促しています。これにより、完全に死に絶えてしまうことを防ぎます。
コード解説
以下が、今回実装した全コードです。
#include <SPI.h>
const int latchPin = 10;
byte world[8];
const byte numFonts[4][8] = {
{0x08, 0x0C, 0x08, 0x08, 0x08, 0x08, 0x1C, 0x00}, // 1
{0x1C, 0x22, 0x20, 0x10, 0x08, 0x04, 0x3E, 0x00}, // 2
{0x1C, 0x22, 0x20, 0x18, 0x20, 0x22, 0x1C, 0x00}, // 3
{0x10, 0x18, 0x14, 0x12, 0x3F, 0x10, 0x10, 0x00} // 4
};
enum Rule { MAZE, CORAL, SEEDS, CLASSIC };
Rule currentRule = MAZE;
unsigned long lastRuleChange = 0;
const unsigned long RULE_DURATION = 10000;
int generationCount = 0;
void setup() {
SPI.begin();
pinMode(latchPin, OUTPUT);
randomSeed(analogRead(0));
showNumber(1);
initWorldRandom();
}
void loop() {
if (millis() - lastRuleChange > RULE_DURATION) {
lastRuleChange = millis();
currentRule = (Rule)((currentRule + 1) % 4);
showNumber((int)currentRule + 1);
initWorldRandom();
}
// 描画(少し速くしてキビキビ動かす)
for (int step = 0; step < 10; step++) {
displaySolid();
}
calculateNextGen();
generationCount++;
// 【重要】5世代ごとに画面全体を1ピクセル横にシフトさせる
// これにより「動かない形」が強制的に崩され、永遠に動きが続きます
if (generationCount % 5 == 0) {
shiftWorld();
}
// 強めのノイズ注入(時々新しい生命の種をまく)
if (random(100) < 10) {
world[random(8)] ^= (1 << random(8));
}
}
// 画面全体を横に1ピクセルずらす(端はループ)
void shiftWorld() {
for (int i = 0; i < 8; i++) {
byte lastBit = (world[i] >> 7) & 1;
world[i] = (world[i] << 1) | lastBit;
}
}
void initWorldRandom() {
// 初期値の密度をルールごとに変える
byte density = (currentRule == SEEDS) ? 10 : 80; // 増殖系は少なめから
for (int i = 0; i < 8; i++) world[i] = (random(255) < density) ? random(255) : 0;
}
void calculateNextGen() {
byte nextWorld[8] = {0};
int aliveCount = 0;
bool changed = false;
for (int y = 0; y < 8; y++) {
for (int x = 0; x < 8; x++) {
int neighbors = countNeighbors(x, y);
bool alive = (world[y] >> x) & 1;
bool nextAlive = false;
switch (currentRule) {
case MAZE: nextAlive = alive ? (neighbors >= 1 && neighbors <= 4) : (neighbors == 3); break;
case CORAL: nextAlive = alive ? (neighbors >= 4 && neighbors <= 8) : (neighbors == 3); break;
case SEEDS: nextAlive = (neighbors == 2); break; // 爆発的な増殖(SEEDSルール)
case CLASSIC: nextAlive = alive ? (neighbors == 2 || neighbors == 3) : (neighbors == 3); break;
}
if (nextAlive) {
nextWorld[y] |= (1 << x);
aliveCount++;
}
}
}
for (int i = 0; i < 8; i++) {
if (world[i] != nextWorld[i]) changed = true;
world[i] = nextWorld[i];
}
// 動きが止まったら強制リセット
if (!changed || aliveCount == 0 || aliveCount > 62) {
initWorldRandom();
}
}
int countNeighbors(int x, int y) {
int count = 0;
for (int dy = -1; dy <= 1; dy++) {
for (int dx = -1; dx <= 1; dx++) {
if (dx == 0 && dy == 0) continue;
if ((world[(y + dy + 8) % 8] >> ((x + dx + 8) % 8)) & 1) count++;
}
}
return count;
}
void displaySolid() {
for (int row = 0; row < 8; row++) {
digitalWrite(latchPin, LOW);
SPI.transfer(1 << row);
SPI.transfer(world[row]);
digitalWrite(latchPin, HIGH);
delay(2);
}
}
void showNumber(int num) {
int idx = num - 1;
for (int flash = 0; flash < 2; flash++) {
unsigned long st = millis();
while(millis() - st < 400) {
for (int row = 0; row < 8; row++) {
digitalWrite(latchPin, LOW);
SPI.transfer(1 << row);
SPI.transfer(numFonts[idx][row]);
digitalWrite(latchPin, HIGH);
delay(2);
}
}
digitalWrite(latchPin, LOW); SPI.transfer(0); SPI.transfer(0); digitalWrite(latchPin, HIGH);
delay(100);
}
}
コードのポイント
1. SPI通信で2バイト送信
digitalWrite(latchPin, LOW);
SPI.transfer(1 << row); // 1バイト目:行選択(どの行を点灯させるか)
SPI.transfer(world[row]); // 2バイト目:列パターン(その行のどの列を点灯させるか)
digitalWrite(latchPin, HIGH);
SPI通信で2バイト送ると、74HC595が2個カスケード接続されている場合、最初のバイトが2個目のICへ、2番目のバイトが1個目のICへ送られます。
2. 周囲8マスのカウント
int countNeighbors(int x, int y) {
int count = 0;
for (int dy = -1; dy <= 1; dy++) {
for (int dx = -1; dx <= 1; dx++) {
if (dx == 0 && dy == 0) continue; // 自分自身は除外
if ((world[(y + dy + 8) % 8] >> ((x + dx + 8) % 8)) & 1) count++;
}
}
return count;
}
2次元セル・オートマトンでは、各セルは 周囲8マス(上下左右+斜め4方向) を見て、次の状態を決めます。
(y + dy + 8) % 8 という計算は 端のラップアラウンド(ループ) を実現しています。例えば、y=0のセルが上(dy=-1)を見ると、y=-1ではなくy=7(一番下)を見ることになります。これにより、8×8の世界がドーナツ型(トーラス) のように繋がります。
3. ビット演算で高速化
byte world[8]; // 8行×8列=64ビット=8バイト
bool alive = (world[y] >> x) & 1; // x列目のビットを取得
nextWorld[y] |= (1 << x); // x列目のビットを立てる
8×8のマス目を、8行分のbyte配列で表現しています。各行は8ビット(1バイト)なので、ビット演算で高速に状態を管理できます。
使用部品と購入リンク
ドットマトリクスLEDシールド基板(推奨)
今回使用している自作基板は、74HC595×2、ドライバIC、8×8LEDが一体化されたシールド形式です。
オープンソース版(無料):

GitHubで公開中の回路図・基板データ
回路図、基板データ、プログラムはすべてGitHubで公開しています。JLCPCBでそのまま実装依頼できます。
👉 回路図・基板データ(GitHub)
👉 Arduinoプログラム(GitHub)
完成品(BOOTH販売):
🛒 すぐに使える完成キット
セット内容:
- ✅ Arduinoシールド基板(IC・抵抗実装済み)
- ✅ ドットマトリクスLED(OSL641501-ARA)
- ✅ 差し込み用ピンソケット
- ✅ 長ピンソケット(ピン名印字あり)
詳しい設計や製作過程は、74HC595とドットマトリクスLED制御の記事をご覧ください。
Arduino
Arduino UNO R4(またはR3、Nano)が必要です。初心者の方には、必要な部品が全て揃った スターターキット がおすすめです。
自作する場合の部品リスト
基板を自作したい方向けに、個別部品のリンクも掲載しておきます。
74HC595シフトレジスタ

74HC595(秋月電子)
8×8ドットマトリクスLED

8x8ドットマトリクスLED(OSL641501-ARA)
ドライバIC
- TBD62783(アノードドライバ)
- TBD62083(カソードドライバ)
これらは秋月電子やマルツ電波などで入手可能です。
注意: ドットマトリクスLEDを明るく点灯させるには、74HC595の出力電流だけでは不足するため、ドライバICが必須です。
まとめ:小さなドットに宿る生命
「たった8×8」と侮るなかれ。ルールと少しの「ゆらぎ」を加えるだけで、プログラミングの奥深さを視覚的に楽しむことができました。
このプロジェクトで学べること
- 74HC595によるピン拡張: たった3本でLEDマトリクスを制御
- ダイナミック点灯: 残像効果を使った表示技術
- セル・オートマトンのアルゴリズム: 単純なルールから生まれる複雑な世界
- ビット演算: メモリ効率の良いデータ管理
- グローバル・ドリフト: 小さな画面でも動き続ける工夫
前回の1次元セル・オートマトンでは「Rule 30」などの1次元を扱いましたが、今回の 2次元 では周囲8マスを見るため、より生命らしい振る舞いが生まれます。
また、74HC595とドットマトリクスLEDの基礎の記事では、基本的な制御方法を解説していますので、合わせてご覧ください。
さらに発展させるには?
- 16×16以上の大きな画面: より複雑なパターンを観察
- カラーLED: ルールごとに色を変える
- パラメータ調整: ノイズ確率やシフト周期を可変に
- 3次元セル・オートマトン: LEDキューブで立体的な生命シミュレーション
単純なルールから生まれる複雑な世界。それが セル・オートマトン の魅力です。ぜひ、あなたも「8×8の小宇宙」を作ってみてください!






